🌵1. CNN特点
假设一批图片样本，图片尺寸都是100 × 100（单通道）。使用神经网络来进行训练，假设第一个隐藏层有2500个神经单元，则参数个数一共为 10000 × 2500 = 2500W
存在的问题：
- 参数数据量太多，需要大量的计算资源
- 图片是一个二维结构，相邻像素之间的关联较强，距离远的像素之间关联较弱，因此不必要一次性把所有像素在一起计算
CNN可以很好地解决这两个问题，其基本特点是：
- 权值共享
- 局部连接
2. 卷积
卷积是一种数学运算，定义可以参考wiki。在CNN中，主要关注离散卷积。关于离散卷积的例子，可以参考 如何通俗易懂地解释卷积？- 马同学的回答。CNN中的卷积操作和数学上的定义类似，但并不完全一致（相乘的顺序不同）。
卷积核即filter，用来对图像进行特征提取。计算规则如图所示：
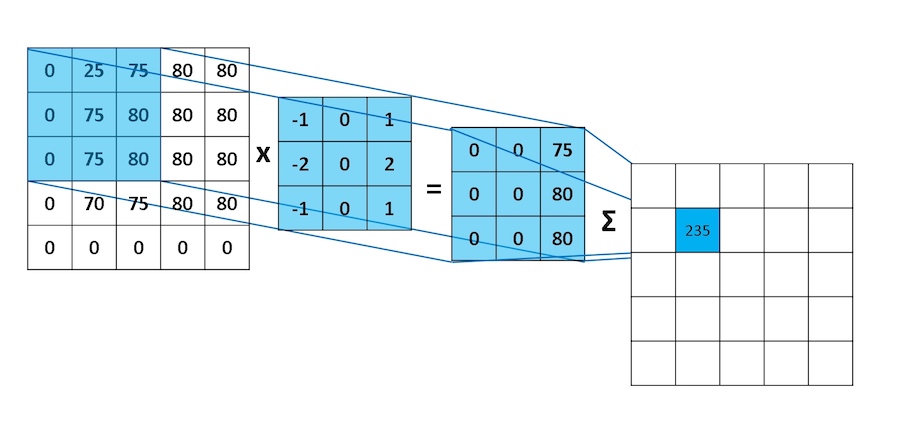
假设图片尺寸为 ，filter尺寸为 ，则卷积操作后的尺寸为
3. Padding
上面的操作存在的不足：
- 每次卷积操作都会使图像缩小
- 角落和边缘区域的像素点使用的很少，即丢失了图像边缘位置的信息
为了解决这两个问题，在卷积操作之前，先对图像周围进行填充，通常为zero-padding，即填充0。
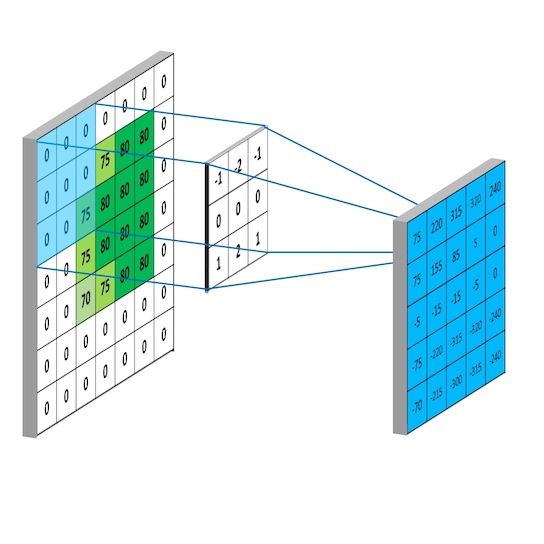
常用的填充方式为：
- Valid：不填充
- Same：输出尺寸和输入尺寸一致
filter尺寸通常为奇数：方便same padding
4. Stride
filter每次移动多个像素。此时输出尺寸为：
5. Channel
对于RGB图像，有三个色彩通道，此时filter不再是二维，而是一个三维的结构。
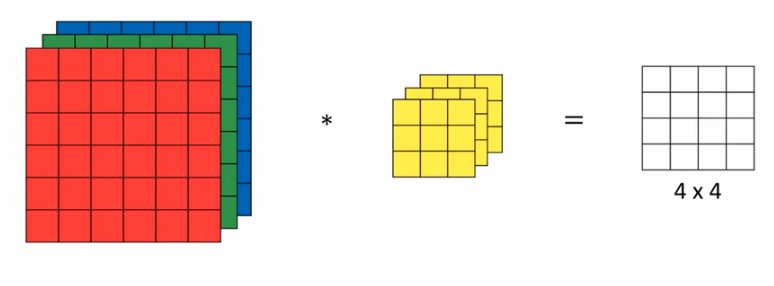
- 输入尺寸
- filter尺寸
- 输出尺寸
假设filter的个数为 ，则最后输出的尺寸为
6. 卷积层的符号表示
- filter size:
- padding:
- stride:
- number of filters:
- input:
- output: ，其中 ,
- each filter:
- activations: ,
- weights:
- bias:
7. Pooling
- 提高计算速度
- 提高所提取的特征的有效性
参数：尺寸 ，步长
pooling方法有：
- max pooling
- average pooling
常用的是max pooling：
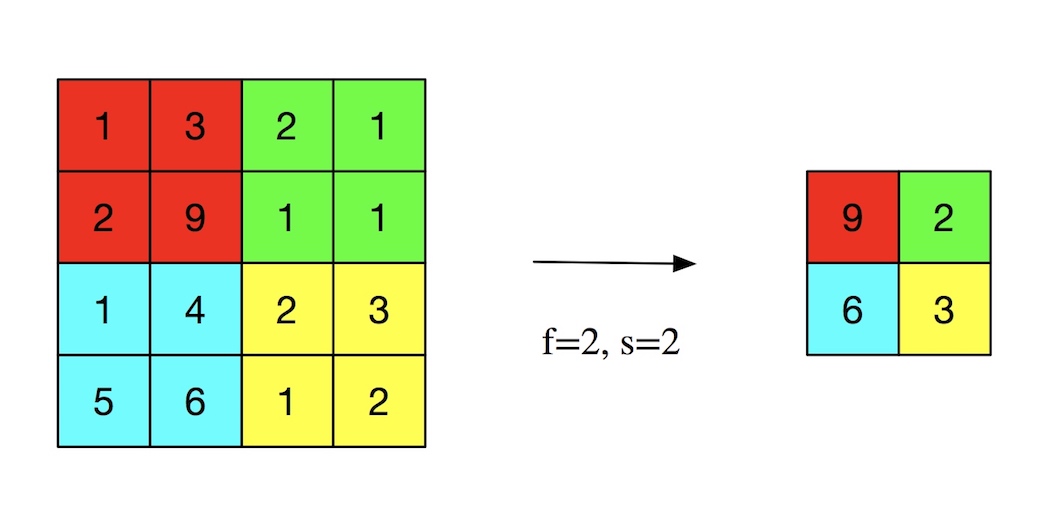
8. CNN一般结构
- 卷积层（CONV）
- 池化层（POOL）
- 全连接层（FC）