🌵1. Sigmoid
线性回归针对的是连续值，逻辑回归则是针对离散的分类问题。如图所示：
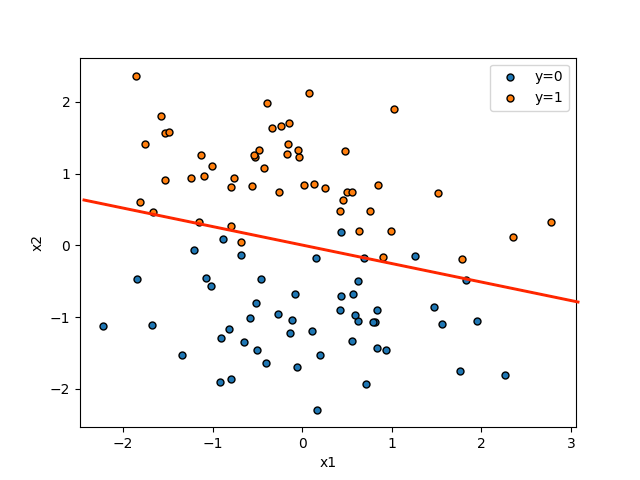
需要注意的是，虽然绘图是在二维平面内，但是数据其实是有三个维度：， 和 。假设：
则：
令：
如图：
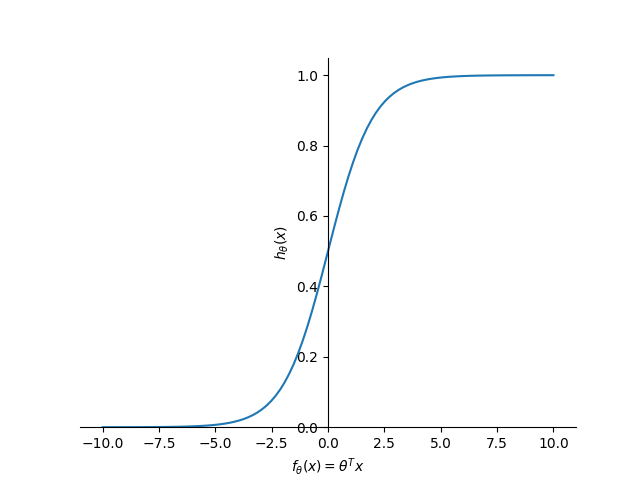
则：
2. Cost Function
令：
图像如下：
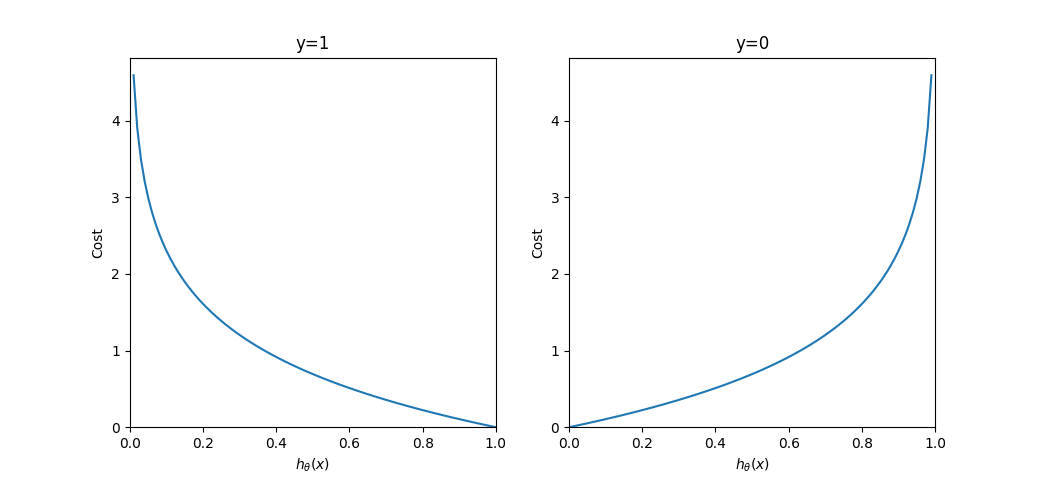
- 时
- 若 ，则
- 若 ，则
- 时
- 若 ，则
- 若 ，则
将以上两种情况统一起来，可以得到：
令：
运行梯度下降，即对于 ：
在只有一个样本的情况下：
TIP
对于 Sigmoid 函数：
由于：
因此：
因此对于 ：
与线性回归的形式是一致的。
3. 多类分类
假如一共有 类，如果求某个样本属于第 类的可能性，则将 类作为是 ，其它 类作为是 。因此：
对于一个样本 ，选取最大的 ，则该样本属于第 类。