1. 模型选择
对于一组数据集，可能会选择不同的模型。例如：
将数据随机分为三部分：
- 训练集（training set）60%：用于训练模型
- 交叉验证集（cross validation set）20%：用于选择模型
- 测试集（test set）20%：用于估计模型的泛化误差
即将数据分成三部分后，用训练集来训练出 （ 表示多项式次数）；然后选择 使得 最小。
2. bias & variance
bias 为偏差，variance 为方差。下图：
- 左图为欠拟合，会导致偏差很大
- 中间图为刚好拟合
- 右图为过拟合，会导致偏差很小，但是方差很大
（1）多项式次数
下面是随着多项式次数的变化， 的变化情况：
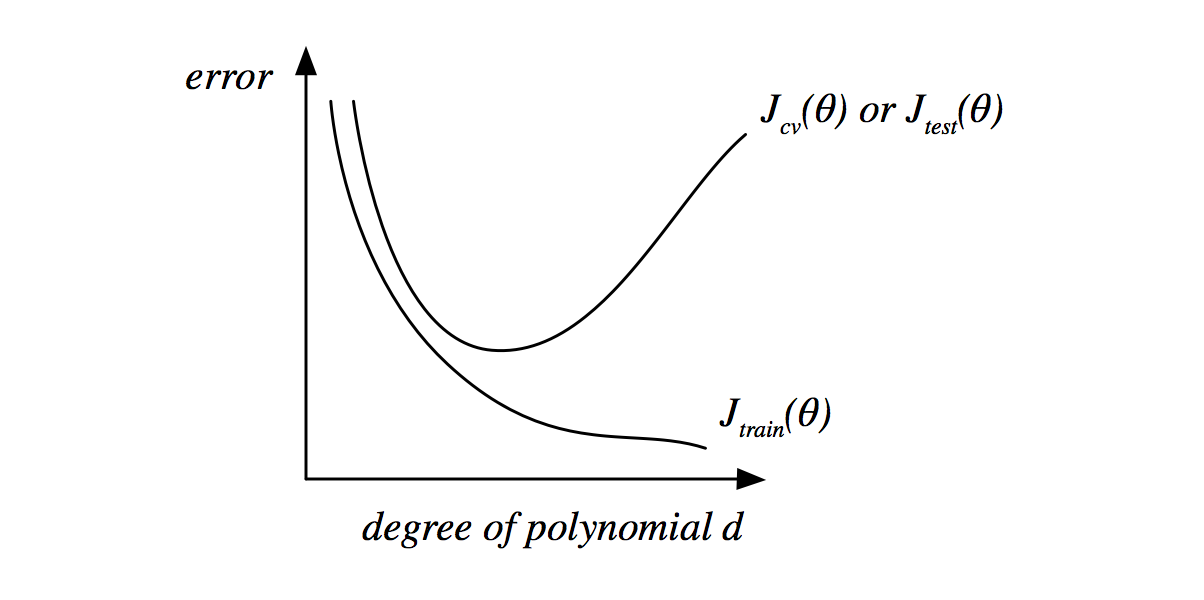
最左边是欠拟合状态，因此训练集和验证集的误差都很大；右边是过拟合状态，训练集的误差很小，而验证集的误差很大。
（2）正则化
在正则化的情况下：
- 如果 很大，则 ，欠拟合，偏差很大
- 如果 很小，则容易过拟合，方差很大
图像如下：
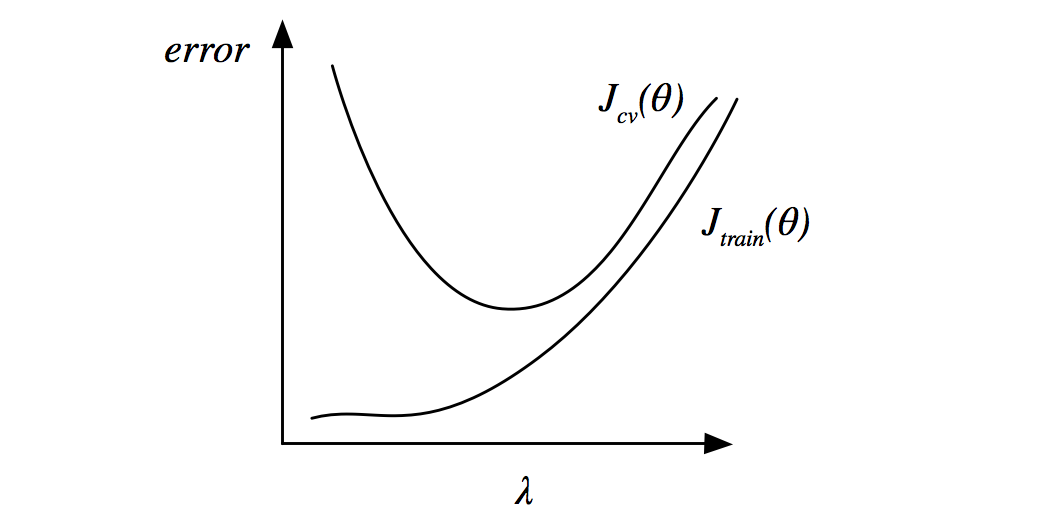
（3）样本数
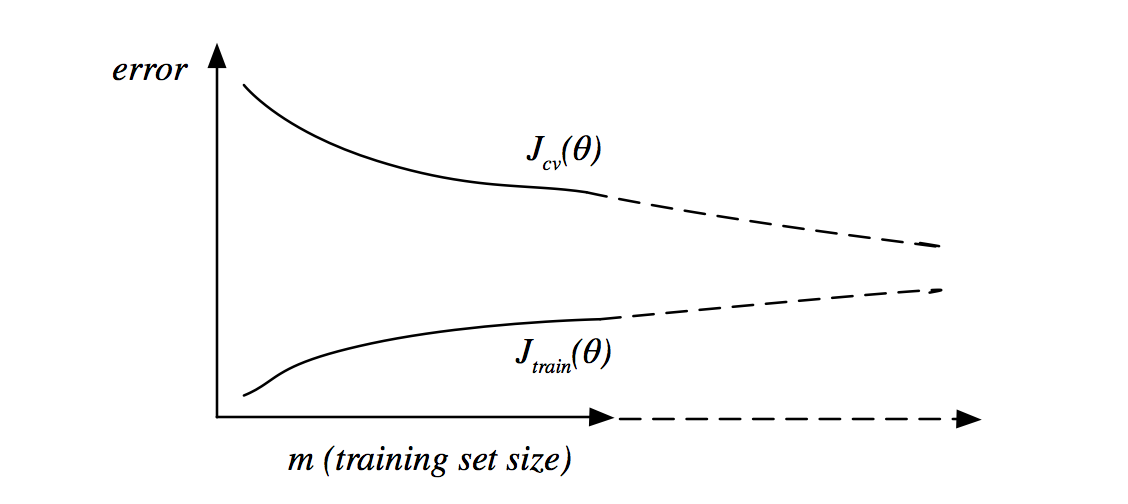
在样本数很小的情况下，模型很容易就拟合的很好，因此训练集误差很小，但是由于这样很难泛化，因此交叉验证集误差很大。随着样本数逐渐增多，训练集误差逐渐增大，交叉验证误差也逐渐减小。如图所示：
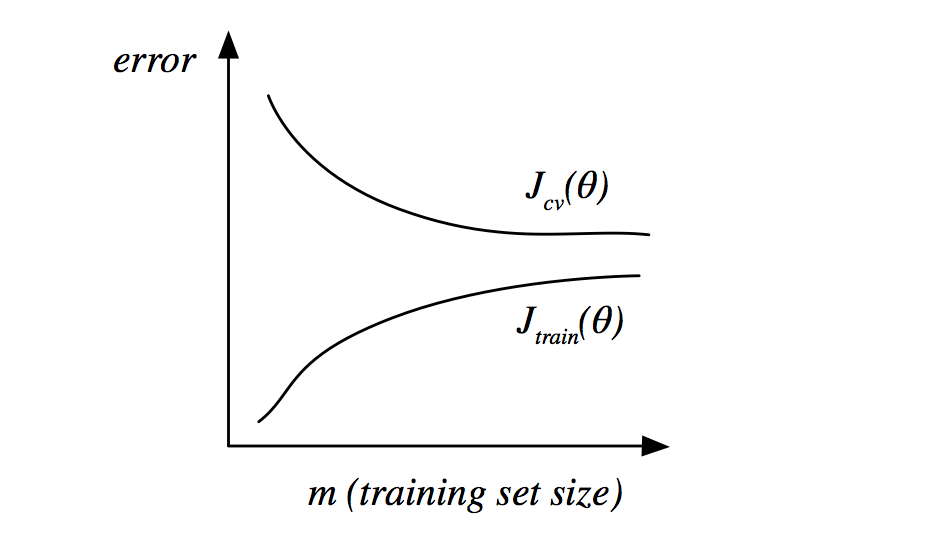
在欠拟合的情况下，随着样本数的增加，训练集和交叉验证集的误差都会相对较大，并且训练集误差会趋近于交叉验证集误差。在这种情况下，随着样本数增加，交叉验证集的误差会逐渐平缓。因此在欠拟合情况下，增加样本数并不能解决问题。如图所示：
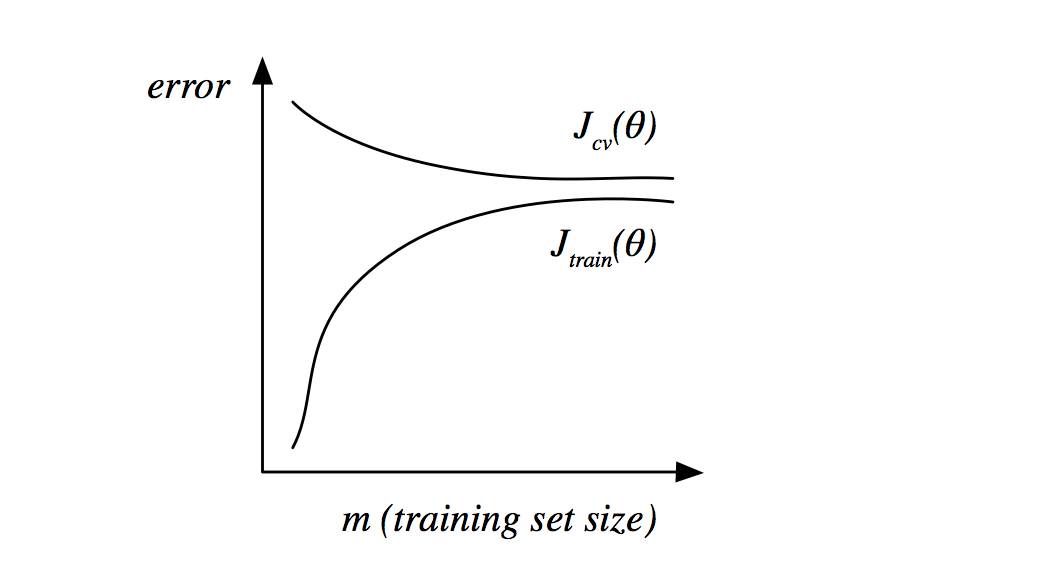
在过拟合的情况下，随着样本数增加，训练集误差虽然会增加，但是一直处于相对较小的状态，交叉验证集误差会逐渐下降，但是误差会相对较大。在这种情况下，如果继续增加样本数，交叉验证集误差会继续减小。因此在过拟合情况下，增加样本数是可以在一定程度上解决问题的。如图所示：
3. 偏斜类
假设通过逻辑回归来预测病人是否有癌症。 表示没有癌症， 表示有癌症。如果我们在测试集进行测试，得到最终只有 1% 的错误率，可能会认为是一个不错的结果。但是考虑到如下情况：癌症的样本数只有 0.5%。那么即使我们忽略样本的特征，直接返回 ，也才只有 0.5% 的错误率。因此在正负样本比例悬殊的情况下，就会产生偏斜类的问题。
在有偏斜类的情况下，使用 和 来计算模型的准确率。
| Actual 1 | Actual 0 | |
|---|---|---|
| Predict 1 | True Positive | False Positive |
| Predict 0 | False Negative | True Negative |
则 可以表示在预测的有癌症患者中，有多少人是真的有癌症的。即：
表示的是在所有患有癌症的病人中，预测出患有癌症的比例是多少。即：
在具体的案例中，会选择不同的 ，当 的时候，才会预测 。
针对不同的模型，为了比较它们的准确度，使用 ：
其中 表示 ， 表示 。