1. K-Means

K-Means 是一种聚类算法，属于无监督学习。其算法非常简单。

输入是：

• 聚类数
• 样本

算法过程：

1. 随机初始化 个聚类的中心点
2. 重复如下过程：
   1. 对于每个样本，选择离该样本最近的聚类中心点 ，将该样本标记为第 类
   2. 对于每个聚类，更新该聚类的中心点 为所有该聚类的点的中心

可视化过程如图：

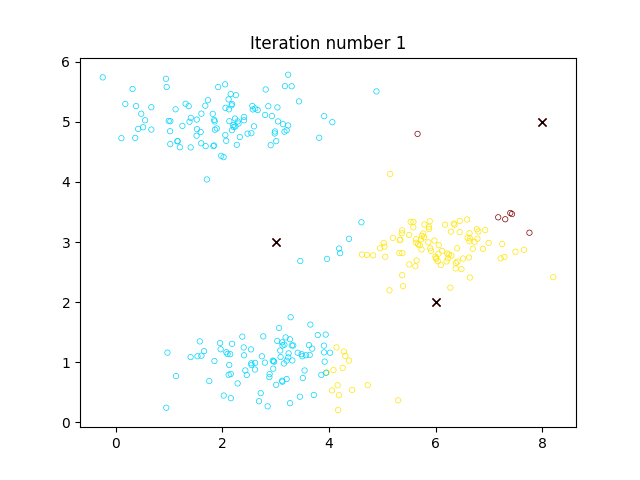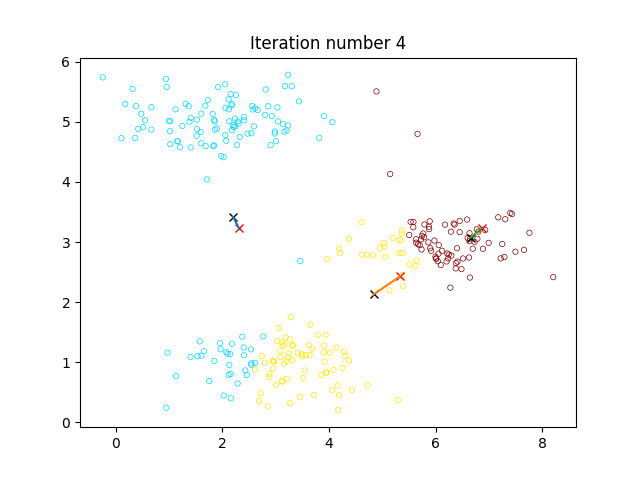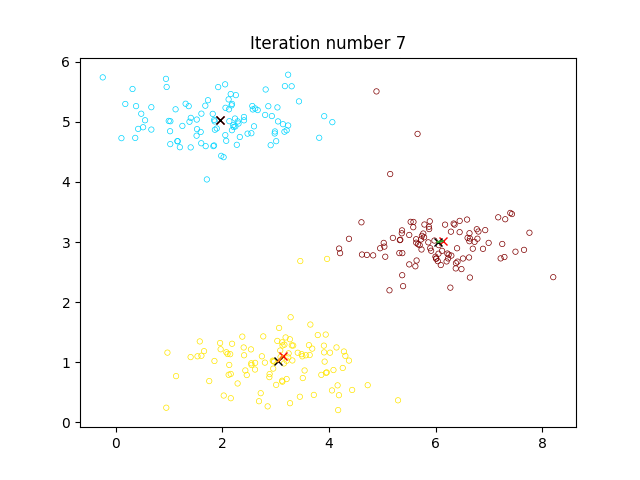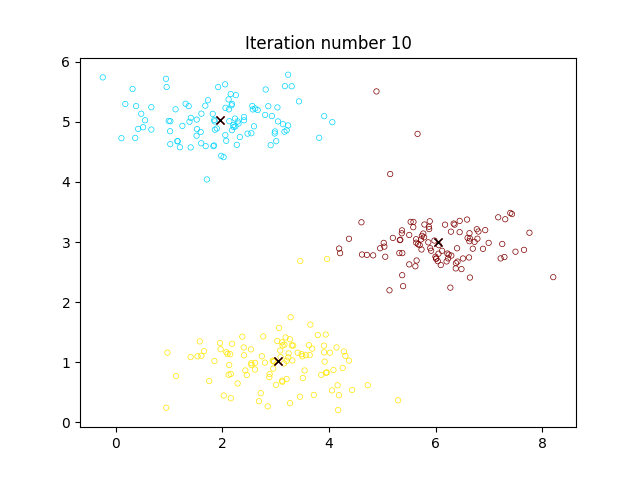
2. 优化目标

令：

• 表示第 个样本当前所属聚类（ 可取值为 ）
• 表示第 个聚类的中心
• 表示第 个样本当前所属聚类的中心

则代价函数：

因此需要：

通过分析上面的算法过程，不难发现：

• 2.1 其实就是在保持 不变的情况下，通过调整 ，来使 减小
• 2.2 其实就是在保持 不变的情况下，通过调整 ，来使 减小

3. 初始化聚类中心

通常会从样本中随机选择 个作为初始的聚类中心。但是不同的初始化可能导致不同的结果。例如：

也就是说，有可能只是得到了局部最优，而没有得到全局最优。

一个可行的方法是：多次随机初始化聚类中心，然后运行 K-Means 算法，得到 ，然后选取最小的 。

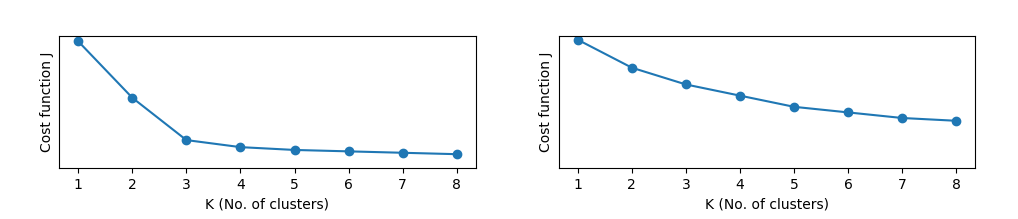
4. 选择聚类数目

至于聚类数目 的选定，有如下方法：

• 肘部法则 (Elbow Method)
• 人工手动设定

“肘部法则”即通过 和 的关系图，来找到明显的拐点（如下图左 ），但是有时候并没有明显的拐点（如下图右）。在实际场景中，很多情况下是根据聚类后的数据需求，来人工手动设置聚类数目。