🌵1. 正态分布（高斯分布）
假设对于一组数据 ，如果它们满足正态分布，且平均数为 ，方差为 ，则记作：
概率密度函数为：
图像如下：
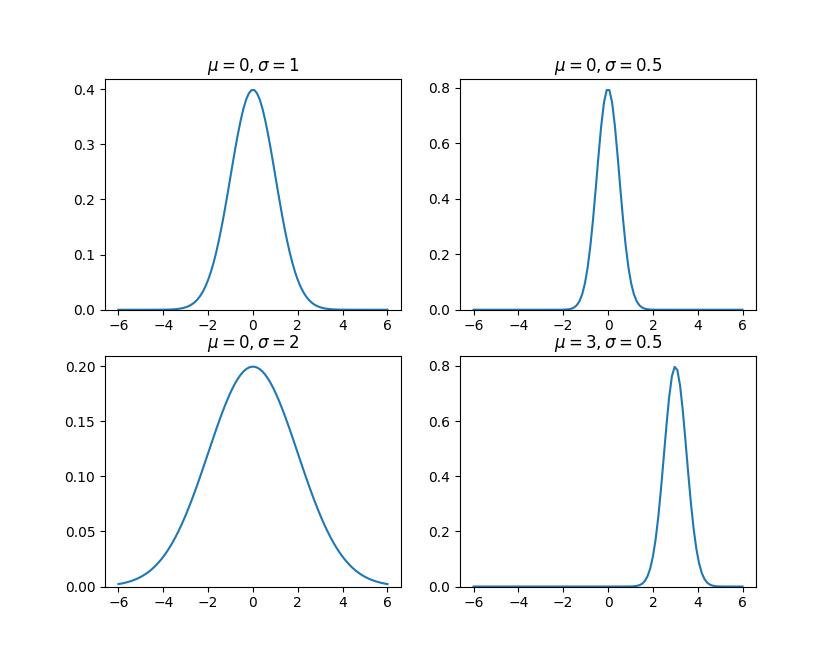
如果 ，则为标准正态分布。
2. 异常检测
假设有 个样本，每个样本有 个特征。在每个特征符合独立的正态分布的情况下，首先计算：
则：
若 （其中 是一个给定的较小的值），则认为该样本属于异常点。
如果一个特征不符合正态分布的话，需要做一些处理，使其基本符合正态分布。比如：
3. 多元高斯分布
上面的方法是假设所有的特征都符合相对独立的正态分布。如图所示：
然而事实上，许多情况下，不同特征之间是有着一定的关系的，并不是完全独立，因此上面的方法不再适用。如下图所示：
如果按照特征相对独立的方式来检测异常，将会是红色的圈，那么检测不到红色的点为异常。然而实际上应该是绿色的圈，这样才能检测到红色的点为异常。
此时需要计算协方差。即：
然后：