🌵1. 维数约减
有时候样本的特征数有许多，其中会有一些冗余的特征。因此需要通过维数约减（Dimensionality Reduction）用更少的特征来表示样本。好处是：
- 节省计算资源
- 提高算法运行速度
例如将二维数据 用一维数据 来表示：
将三维数据映射到二维：
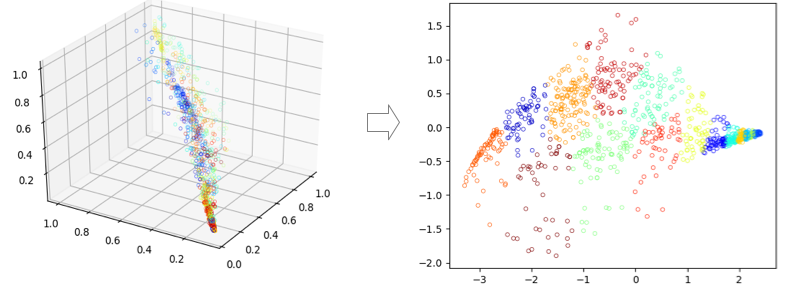
2. PCA
PCA 即主成分分析（Principal Component Analysis），是维数约减常用的一种方法。
首先是对数据进行预处理：
- 使每个特征的平均值为0，即对于每个特征，计算 ，然后令
- 如果不同特征之间的数量级差别很大，还需要进行特征缩放，参考线性回归的特征标准化
然后要将 维数据约减为 维:
首先求协方差矩阵：
可以得知协方差矩阵 是一个 的对称矩阵。
接下来求该协方差矩阵的特征向量，使用 svd （Singular Value Decomposition，即奇异值分解）：
得到的 是一个 的矩阵：
选取 的前 列，记作：
记维度约减后每个样本为 ，则：
即：
3. Reconstruction
通过上面的步骤将数据进行了压缩，同样，可以通过逆向流程来恢复数据。由于：
因此：
之所以用 ，是因为恢复后的数据会有一定的误差。如下图所示，左边为原始数据，右边为恢复后的数据。
4. 选择主成分数量
约减后的维度数 又称为主成分数量。那么应该如何选择 呢？选择最小的 ，使得：
这里选择0.01，可以保证99%的差异性得以保留。
但是如果从 开始，逐个尝试的话，效率会很低。考虑到之前求协方差矩阵的特征向量的时候：
此处 是一个对角矩阵：
并且：
因此找到最小的 ，使得：