1. 优化目标

SVM 即支持向量机（Support Vector Machines），是一种大间距分类算法。

回顾在逻辑回归中，一个样本的损失函数为：

即：

• 当 时：
• 当 时：

函数图像如下：

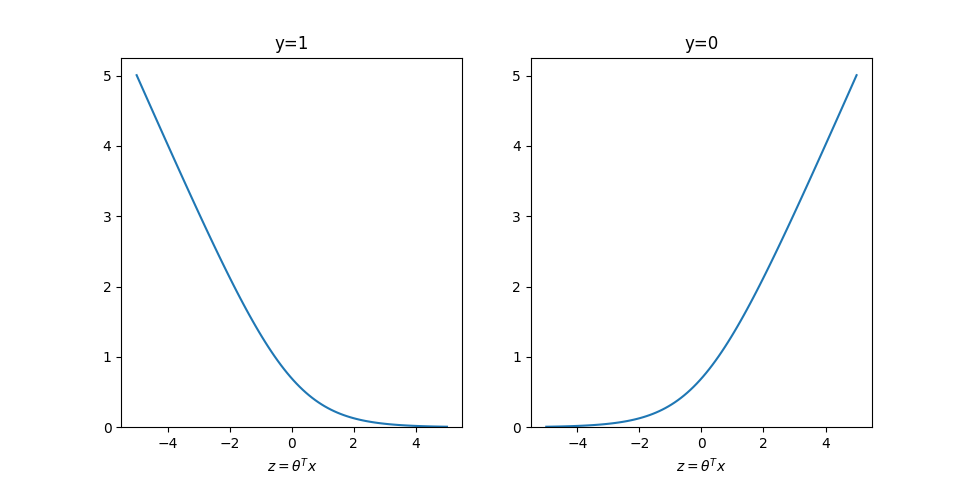
回顾在逻辑回归中：

• 当 时，需要
• 当 时，需要

现在我们用另一个图像来近似拟合上面的损失函数，来得到一个更加严格的约束：

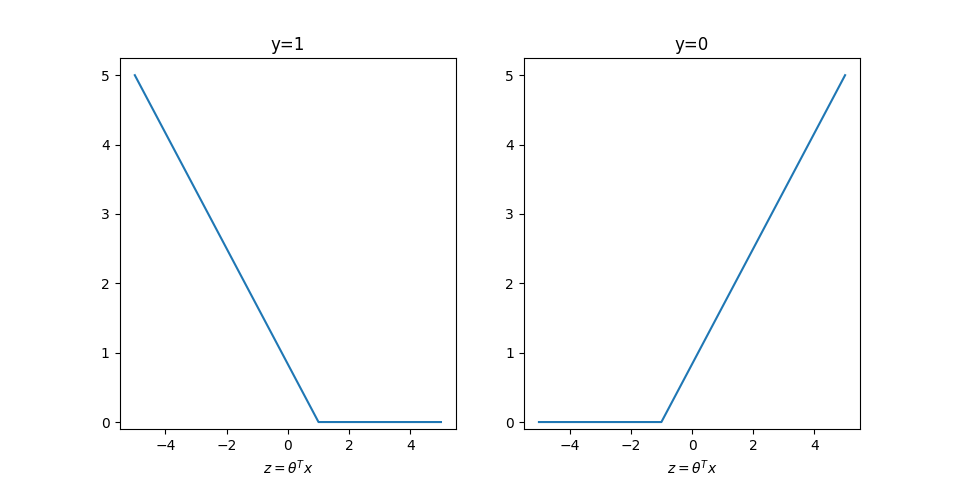
因此：

• 当 时，需要
• 当 时，需要

我们记 的损失函数为 ，记 的损失函数为 。令 SVM 的优化目标为：

假设将 设置的比较大，那么我们希望：

因此我们的优化目标为：

2. 大间距分类

SVM 能够很好地进行大间距分类。如图：

图中，三条线都能够将两类分开，但是很明显，实线比另外两条虚线划分的更好。因为两个类别的样本到实线的距离相对较大，而到虚线的距离相对较小，因此容易误判。

在数学上，两个向量点乘：

其中：

• 表示向量 在向量 方向上投影的长度
• 表示向量 的长度

因此：

其中 表示 在 方向的投影长度。我们知道 为分界线的法向量反向，因此 可以在一定程度上反映 到分割线的距离。因此我们希望 尽量大，也就是 尽量小。而：，因此这也就与前面的优化目标相一致了。

3. Gaussian Kernel

上面的分析我们假设都是线性可分的，然而实际上许多情况并非是线性可分。在这种情况下，我们可以通过将样本特征通过一定的函数映射，转化为线性可分。这里以高斯核为例。

将样本的 个特征映射为新的 个特征 。首先我们先选择 个点 ，定义：

• 若 ，则
• 若 离 很远，则

下面是当 时， 的图像：

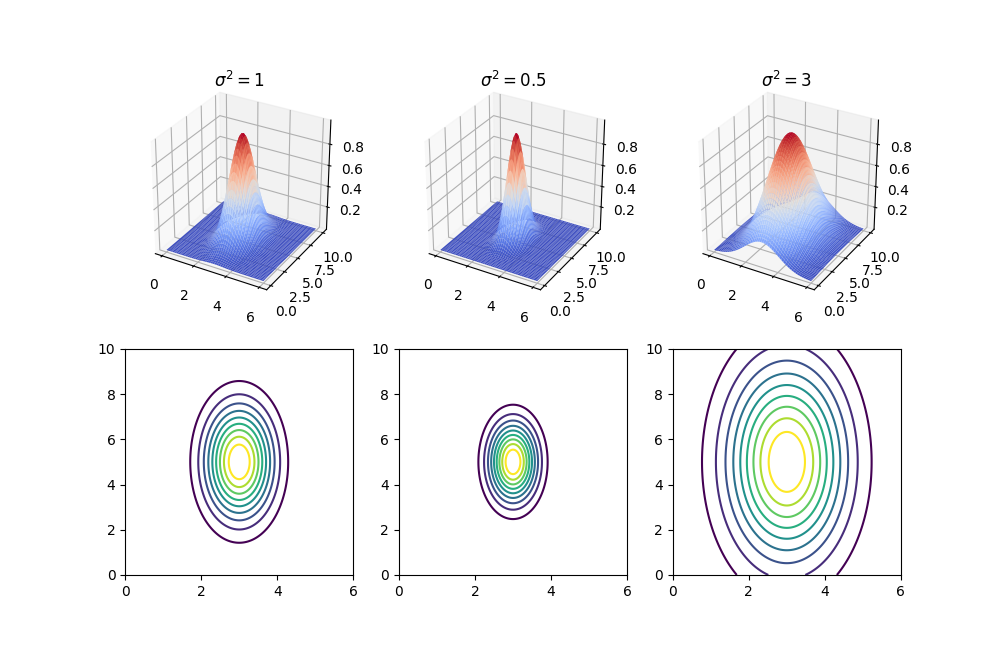
在得到这些新的特征后，我们对这些新的特征使用 SVM。

在实际过程中，如何选择参照点 呢？实际上，可以直接将 个样本点作为 个参照点，即：