1. 前向传播

如上图，左边为一个简单的神经网络结构，右边为每一个神经单元的计算过程。

对于一个样本：

其中：

一般来说，令：

• 表示神经网络层数（不包含输入层），输入层看作是第0层
• 表示第 层的节点数量
• 表示第 层的激活函数

则对于多个样本向量化：

2. 激活函数

• 不同的层可以使用不同的激活函数
• 激活函数是非线性的

常用的激活函数有：

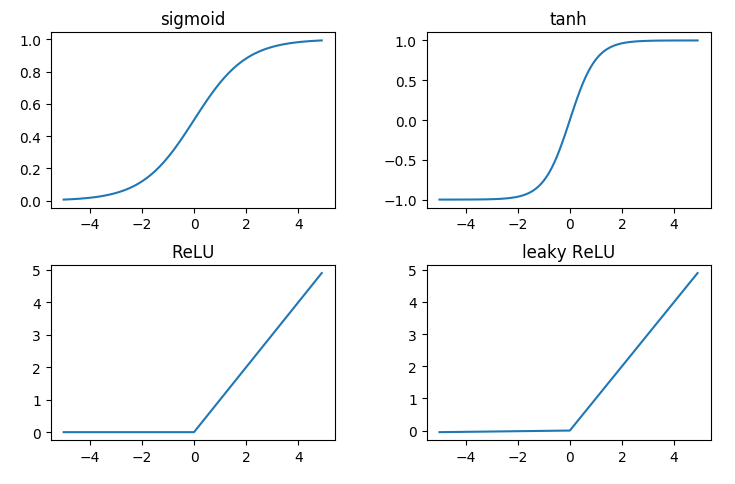
它们的导数分别为：

3. 反向传播

在前向传播过程中，针对每一层，输入为 ，输出为 ：

在反向传播过程中，针对每一层，输入为 ，输出为 ，，：

4. 参数初始化

在逻辑回归中，参数 和 可以都初始化为0，但是在神经网络中，如果这样做的话，则每一层所有的神经单元都是在做着同样的计算。因此需要进行随机初始化。

初始化的参数值通常会很小。如果比较大，在使用了sigmoid或者tanh激活函数的时候，计算值就容易落到函数值较大的区域，从而梯度很小，导致反向传播过程进行的很慢。

5. 参数和超参数

参数：

超参数：

• 学习速率
• 梯度下降迭代次数
• 神经网络层数
• 每一层的节点数
• 激活函数类型
• ……

超参数决定了最终训练好的参数 和 的值，即超参数是控制参数的参数。